GABRIEL RIOS DIAZ
DAVID DOMINGUEZ MORA
1 BIMESTRE
Al-Jwarizmi (780-835), matemático árabe, nacido en Jwrizm (actualmente Jiva, Uzbekistán). Fue bibliotecario en la corte del califa al-Mamun y astrónomo en el observatorio de Bagdad. Sus trabajos de álgebra, aritmética y tablas astronómicas adelantaron enormemente el pensamiento matemático y fue el primero en utilizar la expresión al jabr (de la que procede la palabra álgebra) con objetivos matemáticos. La versión latina (por el traductor italiano Gerardo de Cremona) del tratado de al-Jwrizm sobre álgebra fue responsable de gran parte del conocimiento matemático en la Europa medieval. Su trabajo con los algoritmos (término derivado de su nombre) introdujo el método de cálculo con la utilización de la numeración arábiga y la notación decimal.TEMAS 1 BIMESTRE
SUMA DE POLINOMIOS :
Para sumar dos polinomios se suman los coeficientes de los
términos del mismo grado.
Ejemplo: suma 2x2 + 6x + 5 y 3x2 - 2x - 1
Junta los términos similares: 2x2 + 3x2 + 6x - 2x + 5 - 1
Suma los términos similares: (2+3)x2 + (6-2)x + (3-1)
= 5x2 + 4x + 4
RESTA DE POLINOMIOS :
La resta de polinomios consiste en sumar al minuendo el
opuesto del sustraendo.
A = - 3x2 + 9x4 - 8 - 4x3 + 1/2 x
B = 5x4 - 10 + 3x + 7x3
9x4 - 4x3 - 3x2 + 1/2 x - 8 (el polinomio A ordenado y completo)
-
5x4 + 7x3 + 0x2 + 3x - 10 (el polinomio B ordenado y completo)
______________________________
La resta se puede tranformar en suma, cambiando todos los signos del segundo polinomio:
9x4 - 4x3 - 3x2 + 1/2 x - 8
+
-5x4 - 7x3 + 0x2 - 3x + 10 (el polinomio B con los signos cambiados)
______________________________
4x4 - 11x3 - 3x2 - 5/2 x + 2
A - B = 4x4 - 11x3 - 3x2 - 5/2 x + 2
B = 5x4 - 10 + 3x + 7x3
9x4 - 4x3 - 3x2 + 1/2 x - 8 (el polinomio A ordenado y completo)
-
5x4 + 7x3 + 0x2 + 3x - 10 (el polinomio B ordenado y completo)
______________________________
La resta se puede tranformar en suma, cambiando todos los signos del segundo polinomio:
9x4 - 4x3 - 3x2 + 1/2 x - 8
+
-5x4 - 7x3 + 0x2 - 3x + 10 (el polinomio B con los signos cambiados)
______________________________
4x4 - 11x3 - 3x2 - 5/2 x + 2
A - B = 4x4 - 11x3 - 3x2 - 5/2 x + 2
2 BIMESTRE
HERON DE ALEJANDRIA (c.
20-62 d.C.), matemático y científico griego. Su nombre también podría ser Hero
(aproximadamente 18 escritores griegos se llamaron Hero ó Herón, creándose
cierta dificultad a la hora de su identificación). Herón de Alejandría nació
probablemente en Egipto y realizó su trabajo en Alejandría (Egipto).
Escribió al menos 13 obras sobre mecánica, matemáticas y física. Inventó varios instrumentos mecánicos, gran parte de ellos para uso práctico: la aelípila, una máquina a vapor giratoria; la fuente de Herón, un aparato neumático que produce un chorro vertical de agua por la presión del aire y la dioptra, un primitivo instrumento geodésico.
Sin embargo, es conocido sobre todo como matemático tanto en el campo de la geometría como en el de la geodesia (una rama de las matemáticas que se encarga de la determinación del tamaño y configuración de la Tierra, y de la ubicación de áreas concretas de la misma).
Herón trató los problemas de las mediciones terrestres con mucho más éxito que cualquier otro de su generación.
También inventó un método de aproximación a las raíces cuadradas y cúbicas de números que no las tienen exactas.
A Herón se le ha atribuido en algunas ocasiones el haber desarrollado la fórmula para hallar el área de un triángulo en función de sus lados, pero esta fórmula, probablemente, había sido desarrollada antes de su época. Inventor y físico francés.
Escribió al menos 13 obras sobre mecánica, matemáticas y física. Inventó varios instrumentos mecánicos, gran parte de ellos para uso práctico: la aelípila, una máquina a vapor giratoria; la fuente de Herón, un aparato neumático que produce un chorro vertical de agua por la presión del aire y la dioptra, un primitivo instrumento geodésico.
Sin embargo, es conocido sobre todo como matemático tanto en el campo de la geometría como en el de la geodesia (una rama de las matemáticas que se encarga de la determinación del tamaño y configuración de la Tierra, y de la ubicación de áreas concretas de la misma).
Herón trató los problemas de las mediciones terrestres con mucho más éxito que cualquier otro de su generación.
También inventó un método de aproximación a las raíces cuadradas y cúbicas de números que no las tienen exactas.
A Herón se le ha atribuido en algunas ocasiones el haber desarrollado la fórmula para hallar el área de un triángulo en función de sus lados, pero esta fórmula, probablemente, había sido desarrollada antes de su época. Inventor y físico francés.
ARQUIMIDES: Nació en el 287 a. C. en Siracusa, Sicilia,
aunque se educó en Alejandría (Egipto).
Arquímedes fue primo del rey Hierón II del cual fue consejero y responsable de la defensa de la ciudad. El empeño del rey Hierón era la construcción de una gran flota e hizo construir el Syrakosa, la mayor nave de su época, que en el momento de su botadura quedó embarrancado. Arquímedes con ayuda de poleas compuestas ayudadas por palancas apuntaladas en el casco consiguió levantarlo a flote ante la fascinación del rey.
Se anticipó a muchos de los descubrimientos de la ciencia moderna, en las matemáticas puras. Fue capaz de demostrar que el volumen de una esfera es dos tercios del volumen del cilindro que la circunscribe. Además, en mecánica, definió la ley de la palanca y es reconocido como el inventor de la polea compuesta. En Egipto inventó el 'tornillo sin fin' para elevar el agua de nivel. Famoso por el descubrimiento de la ley de la hidrostática, también llamado principio de Arquímedes, que establece que todo cuerpo sumergido en un fluido experimenta una pérdida de peso igual al peso del volumen del fluido que desaloja. Se cuenta que este descubrimiento lo hizo mientras se bañaba, al comprobar cómo el agua se desplazaba y se desbordaba.
La mayor parte de la vida de Arquímedes transcurrió en Sicilia, en Siracusa y sus alrededores, y la dedicó a la investigación y los experimentos. Durante la conquista romana de Sicilia se puso a disposición de las autoridades de la ciudad y muchos de sus instrumentos mecánicos se utilizaron en la defensa de Siracusa. Entre la maquinaria de guerra destacan sus inventos de la catapulta y un sistema de espejos que incendiaba las embarcaciones enemigas al enfocarlas con los rayos del sol.
Cuando Siracusa fue conquistada durante la segunda Guerra Púnica, se cree que fue asesinado en 212 a. C. por un soldado romano que le encontró dibujando un diagrama matemático en la arena. Dicen que Arquímedes estaba tan metido en las operaciones que ofendió al intruso al decirle: "No desordenes mis diagramas".
Escribió varias obras:
1. Esfera y cilindro
2. Medida del círculo
3. Gnoides y esferoides
4. Espirales
5. Equilibrio de los planos y sus centros de gravedad
6. Cuadratura de la parábola
7. El arenario
8. Cuerpos flotantes
9. Los lemas
10. El método
Arquímedes fue primo del rey Hierón II del cual fue consejero y responsable de la defensa de la ciudad. El empeño del rey Hierón era la construcción de una gran flota e hizo construir el Syrakosa, la mayor nave de su época, que en el momento de su botadura quedó embarrancado. Arquímedes con ayuda de poleas compuestas ayudadas por palancas apuntaladas en el casco consiguió levantarlo a flote ante la fascinación del rey.
Se anticipó a muchos de los descubrimientos de la ciencia moderna, en las matemáticas puras. Fue capaz de demostrar que el volumen de una esfera es dos tercios del volumen del cilindro que la circunscribe. Además, en mecánica, definió la ley de la palanca y es reconocido como el inventor de la polea compuesta. En Egipto inventó el 'tornillo sin fin' para elevar el agua de nivel. Famoso por el descubrimiento de la ley de la hidrostática, también llamado principio de Arquímedes, que establece que todo cuerpo sumergido en un fluido experimenta una pérdida de peso igual al peso del volumen del fluido que desaloja. Se cuenta que este descubrimiento lo hizo mientras se bañaba, al comprobar cómo el agua se desplazaba y se desbordaba.
La mayor parte de la vida de Arquímedes transcurrió en Sicilia, en Siracusa y sus alrededores, y la dedicó a la investigación y los experimentos. Durante la conquista romana de Sicilia se puso a disposición de las autoridades de la ciudad y muchos de sus instrumentos mecánicos se utilizaron en la defensa de Siracusa. Entre la maquinaria de guerra destacan sus inventos de la catapulta y un sistema de espejos que incendiaba las embarcaciones enemigas al enfocarlas con los rayos del sol.
Cuando Siracusa fue conquistada durante la segunda Guerra Púnica, se cree que fue asesinado en 212 a. C. por un soldado romano que le encontró dibujando un diagrama matemático en la arena. Dicen que Arquímedes estaba tan metido en las operaciones que ofendió al intruso al decirle: "No desordenes mis diagramas".
Escribió varias obras:
1. Esfera y cilindro
2. Medida del círculo
3. Gnoides y esferoides
4. Espirales
5. Equilibrio de los planos y sus centros de gravedad
6. Cuadratura de la parábola
7. El arenario
8. Cuerpos flotantes
9. Los lemas
10. El método
Multiplicación de monomios
La multiplicación de monomios es
otro monomio que tiene por coeficiente el producto de los
coeficientes y cuya parte literal se obtiene multiplicando las potencias que tenga la misma base,
es decir, sumando los exponentes.
axn · bxm = (a · b)xn + m
(5x2 y3 z) · (2 y2 z2) = 10
x2 y5 z3
Multiplicación de
polinomios
Este
tipo de operaciones se puede llevar a cabo de dos formas distitnas.
Mira
la demostración con el siguiente ejemplo:
P(x) =
2x2 − 3 Q(x) = 2x3 −
3x2 + 4x
OPCIÓN
1
1Se multiplica cada monomio del primer
polinomio por todos los elementos del segundo polinomio.
P(x) ·
Q(x) = (2x2 − 3) · (2x3 − 3x2 +
4x) =
= 4x5 − 6x4 + 8x3 − 6x3+ 9x2 − 12x =
= 4x5 − 6x4 + 8x3 − 6x3+ 9x2 − 12x =
2Se suman los monomios del mismo grado.
= 4x5 −
6x4 + 2x3 + 9x2 − 12x
3Se obtiene otro polinomio cuyo grado es la
suma de los grados de los polinomios que se multiplican.
Grado
del polinomio = Grado de P(x) + Grado de Q(x) = 2 + 3 = 5
VIDEO - MULTIPLICACION DE POLINOMIOS
VIDEO DE MULTIPLICACIO DE MONOMIOS
3 BIMESTRE
GAUSS Carl
F. (1777-1855): Matemático alemán nacido en Brunswick y fallecido en Gotinga.
Gauss fue un niño prodigio en matemáticas y continuó siéndolo toda su vida. Hay
quien le considera uno de los tres mayores matemáticos de la historia junto a
Arquímedes y Newton. Su inteligencia superdotada llamó la atención del duque de
Brunswick, quien decidió costearle todos sus estudios, entrando en 1795 en la
universidad de Gotinga. Antes de cumplir los veinte años hizo algunos
descubrimientos importantes, entre los que se incluye el método de los mínimos
cuadrados. Gauss halló un método para construir un polígono equilátero de 17
lados con ayuda de regla y compás, e incluso fue más allá, demostrando que sólo
ciertos polígonos equiláteros se podían construir con ayuda de regla y compás.
Hizo una labor importante en la Teoría de Números. También construyó una
geometría no euclídea, basada en axiomas distintos a los de Euclides, pero se
negó a publicarla. Lovachevski y Bolyai ostentan el honor de su descubrimiento
al publicarla algo más tarde. En 1799 Gauss demostró el teorema fundamental del
álgebra. También demostró que los números se podían representar mediante puntos
en un plano. El 1801 demostró el teorema fundamental de la aritmética. Se
levantó una estatua en su honor en su ciudad natal, que descansa sobre un
pedestal en forma de estrella de 17 puntas, en celebración de su descubrimiento
de la construcción del polígono de 17 lados. Le llamaban Príncipe de las
Matemáticas.
Resumiendo sus aportaciones:
- Teoría de los errores.
- Método general para la resolución de las ecuaciones binomios.
- Ideó un heliotropo, para el envío de señales luminosas en las operaciones geodésicas (operaciones de mediciones terrestres).
- Formuló la Teoría general del magnetismo terrestre.
- Campana de Gauss que es muy utilizada en el cálculo de probabilidades.
- Realizó aportaciones en la electricidad y en el magnetismo.
- El teorema de Gauss-Bonnet
- El método de Gauss para triangular una matriz (y el método de eliminación de Gauss-Jordan).
- El método de Gauss-Seidel (método iterativo para resolver sistemas de ecuaciones lineales).
- El teorema de la divergencia, conocido también como teorema de Gauss (y por teorema de Ostrogradsky-Gauss).
Resumiendo sus aportaciones:
- Teoría de los errores.
- Método general para la resolución de las ecuaciones binomios.
- Ideó un heliotropo, para el envío de señales luminosas en las operaciones geodésicas (operaciones de mediciones terrestres).
- Formuló la Teoría general del magnetismo terrestre.
- Campana de Gauss que es muy utilizada en el cálculo de probabilidades.
- Realizó aportaciones en la electricidad y en el magnetismo.
- El teorema de Gauss-Bonnet
- El método de Gauss para triangular una matriz (y el método de eliminación de Gauss-Jordan).
- El método de Gauss-Seidel (método iterativo para resolver sistemas de ecuaciones lineales).
- El teorema de la divergencia, conocido también como teorema de Gauss (y por teorema de Ostrogradsky-Gauss).
• Conceptos Importantes para recordar : Una
expresión algebraica es aquella en la que se utilizan letras, números y signos
de operaciones. Las expresiones algebraicas se clasifican según su número de
términos. Clases de expresiones algebraicas: . Si una expresión algebraica está
formada por un solo término se llama monomio. Ejemplo: 3ax2 2. Si la expresión
algebraica tiene varios términos se llama polinomio. 3. Cuando un polinomio
está formado por dos términos se llama binomio. Ejemplo: 2x2 + 3xy
LA DIVISIÓN Es la operación que tiene por objeto,
dado el producto de dos factores dividendo y uno de los factores divisor
encontrar otro factor llamado cociente: D = d • C Donde: D es el Dividendo
(producto de los factores “d” y “C”) d es el divisor (factor conocido) C es el
cociente (factor desconocido) Los factores “D”, “d” y “C” pueden ser números,
monomios o polinomios. Leyes que sigue la división:
Ley de signos: el resultado es negativo si la
cantidad de factores negativos es impar, de lo contrario es
positivo. (+) ÷ (+) = + (-) ÷ (-) = + (+) ÷ (-) = - (-) ÷ (+)
Ley de los cocientes de los coeficientes: el
coeficiente del cociente es el cociente de dividir el coeficiente del dividendo
entre el coeficiente del divisor. mx ÷ nxy = (m ÷ n)(x ÷ xy) Donde m y n son
números y n es distinto de cero.
Ley de exponentes: la división de dos o más
potencias de la misma base es igual a la base elevada a la diferencia de las
potencias. Nota: resulta útil y cómodo colocar la división como una expresión
fraccionaria así:
División de monomios : Es la división de un monomio
entre otro, en fracción se trabaja como reducción de múltiplos iguales. Pasos a
seguir: • Se aplica ley de signos • Se divide el coeficiente del dividendo
entre el coeficiente del divisor • Se aplica ley de los exponentes tomando las
letras que no se encuentren como elevadas a cero (nº = 1), y se escriben en
orden alfabético.
En general, la división de un polinomio entre un monomio no es posible. Solo podrá realizarse cuando todos los términos del polinomio sean divisibles por el monomio. Se divide cada uno de los términos del polinomio por el monomio separando los cocientes parciales con sus propios signos. Esta es la Ley Distributiva de la división.
Por ejemplo:
DIVISION DE POLINOMIOS
Para explicar la división de polinomios nos valdremos de un
ejemplo práctico:
P(x) = x5 + 2x3 − x − 8
Q(x) = x2 −
2x + 1
P(x) : Q(x)
A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos huecos en
los lugares que correspondan.
A la derecha situamos el divisor dentro de una caja.
Dividimos el primer monomio del dividendo entre el primer
monomio del divisor.
x5 : x2 = x3
Multiplicamos cada término del polinomio divisor por el
resultado anterior y lo restamos del polinomio dividendo:
Volvemos a dividir el primer monomio del
dividendo entre el primer monomio del divisor. Y el resultado lo multiplicamos
por el divisor y lo restamos al dividendo.
2x4 : x2 = 2 x2
Procedemos igual que antes.
5x3 : x2 = 5 x
Volvemos a hacer las mismas operaciones.
8x2 : x2 = 8
10x − 16 es el resto, porque
su grado es menor que el del divisor y por tanto no se puede
continuar dividiendo.
x3 + 2x2 + 5x + 8 es el cocienteVIDEO DE DIVISION DE MONOMIOS ENTRE MONOMIOS.
VIDEO DE DIVISON DE POLINOMIO ENTRE MONOMIO
4 BIMESTRE
DIOFANTO DE ALEJANDRIA
Nacido en Alejandría, nada se conoce con seguridad
sobre su vida salvo la edad a la que falleció, gracias a este epitafio
redactado en forma de problema y conservado en la antología griega.
Transeúnte, esta es la tumba de Diofanto: los números pueden
mostrar, ¡oh maravilla! la duración de su vida. Su niñez ocupó la sexta parte
de su vida; después, durante la doceava parte, de vello se cubrieron sus
mejillas. Pasó aún una séptima parte de su vida antes de tomar esposa y, cinco
años después, tuvo un precioso niño que, una vez alcanzada la mitad de la edad
de su padre, pereció de una muerte desgraciada. Su padre tuvo que sobrevivirle,
llorándole, durante cuatro años. De todo esto se deduce su edad.
donde x es la edad que vivió Diofanto.
Según esto, Diofanto falleció a la edad de 84 años. Se
ignora, sin embargo en qué siglo vivió. Si es el mismo astrónomo Diofanto que
comentó Hipatia (fallecida
en 415), habría fallecido antes del siglo V, pero si se trata de
personas distintas cabe pensar que vivía a finales de dicho siglo, ya que ni Proclo ni Papo le
citan, lo que resulta difícil de entender tratándose de un matemático que pasa
por ser el inventor del álgebra. En opinión de Albufaraga, Diofanto vivía en los tiempos
del emperador Juliano, hacia 365, fecha que aceptan los
historiadores.
OBRA
El matemático alejandrino debe su renombre a su obra Arithmetica.
Este libro, que constaba de trece tomos de los que sólo se han hallado seis,
fue publicado por Guilielmus Xylander en 1575 a partir de
unos manuscritos de la universidad de Wittenberg, añadiendo el
editor un manuscrito sobre números poligonales, fragmento de otro tratado del
mismo autor. Los libros que faltan parece que se perdieron tempranamente ya que
no hay razones para suponer que los traductores y comentaristas árabes
dispusieran de otros manuscritos además de los que aún se conservan.
En esta obra realiza sus estudios de ecuaciones con variables que toman valores racionales, las ecuaciones diofánticas, aunque no es una obra de carácter teórico sino una colección de problemas. En el uso moderno, las ecuaciones diofánticas son ecuaciones algebraicas con coeficientes enteros, para lo cual se buscan soluciones enteras. El estudio de las ecuaciones diofánticas y de las aproximaciones diofánticas siguen siendo aspectos importantes de la investigación matemática.
Diofanto fue el primer matemático griego que reconoció a las fracciones como números.
]
Notación matemática
Importante fue también su contribución en el campo de la notación. Si bien los símbolos empleados por Diofanto no son como los concebimos actualmente, introdujo importantes novedades como el empleo de un símbolo único para la variable desconocida (στ) y para la sustracción, aunque conservó las abreviaturas para las potencias de la incógnita (δς para el cuadrado, δδς para el duplo del cuadrado, χς para el cubo, δχς para la quinta potencia, etc.).
Análisis diofántico
Actualmente, el análisis diofántico es el área de estudio donde se buscan soluciones enteras para las ecuaciones, y las ecuaciones diofánticas son aquellas ecuaciones polinómicas con coeficientes enteros de las que sólo se buscan soluciones enteras. Por lo general, es bastante difícil decir si una determinada ecuación diofántica tiene solución. La mayoría de los problemas en Aritmetica llevaban a ecuaciones cuadráticas. Diofanto consideró 3 tipos diferentes de ecuaciones de segundo grado:
La razón por la cual él consideró tres casos, mientras que hoy sólo tenemos uno, es que él no tenía ninguna noción de cero y que evitaba los coeficientes negativos, considerando que los números a, b, c eran positivos en cada uno de los tres casos anteriores. Diofanto siempre se quedaba satisfecho con una solución racional y no requería un número entero como solución, aceptando las fracciones como soluciones a sus problemas. Diofanto considera las soluciones negativas y las raíces cuadradas irracionales como "inútiles", "sin sentido" e incluso "absurdas". Para dar un ejemplo concreto, que él llama a la ecuación 4 = 4x + 20 "absurda" porque conduciría a un valor negativo de x. El sólo buscaba una solución en las ecuaciones de segundo gardo. No hay evidencia que sugiera que Diofanto alguna vez se diera cuenta de que podía haber dos soluciones en una ecuación cuadrática. También consideró ecuaciones cuadráticas simultaneas.
FACTORIZACION DE MONOMIOS
La factorización de monomios es muy similar a la
factorización de números. Básicamente consiste en
obtener los factores primos del coeficiente y posteriormente
obtener los factores de las literales, los cuales quedan indicados
por el exponente de cada literal.
Ejemplo. Factorizar el monomio 24xy3z2.
24xy3z2 = 2 • 2 • 2 • 3 • x • y • y • y • z
FACTORIZACON DE POLINOMIOS
Consiste en aplicar la propiedad distributiva:
a · b + a · c + a · d = a (b + c + d)
Ejemplos
Descomponer en factores sacando factor común y hallar las raíces1. x3 + x2 = x2 (x + 1)
La raíces son: x = 0 y x = −1
2. 2x4 + 4x2 = 2x2 (x2 + 2)
Sólo tiene una raíz x = 0; ya que el polinomio, x2
+ 2, no tiene ningún valor que lo anule; debido a que al estar la x al
cuadrado siempre dará un número positivo, por tanto es irreducible.
FACTOR COMUNJ POR AGRUPACION DE TERMINOS
Se llama factor común por agrupación de términos, si los términos de un polinomio pueden reunirse en grupos de términos con un factor común diferente en cada grupo.
Cuando pueden reunirse en grupos de igual número de términos se le saca en cada uno de ellos el factor común. Si queda la misma expresión en cada uno de los grupos entre paréntesis, se la saca este grupo como factor común, quedando así una multiplicación de polinomios.
Tratar desde el principio que nos queden iguales los términos de los paréntesis nos hará mas sencillo el resolver estos problemas.
2ax + 2bx - ay + 5a - by + 5b
Agrupo los términos que tienen un factor común:
(2ax - ay + 5a ) + ( 2bx - by + 5b )
Saco el factor común de cada grupo:
a ( 2x - y + 5 ) + b (2x - y + 5 )
Como las expresiones encerradas entre paréntesis son iguales se tiene:
( 2x -y +5 )(a + b)
Que es nuestra respuesta.
Ejemplos:
17ax – 17mx + 3ay - 3my + 7az – 7mz = a(17x +3y +7z) - m(17x + 3y +7z)
= (17x +3y +7z)(a – m)
m(x + 2) – x – 2 + 3(x + 2) = (x + 2)(m + 3) -1(x + 2) = (x + 2)[(m + 3) – 1]
= (x + 2)(m + 3 – 1)
DIFERENCIA DE CUADRADOS
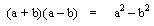
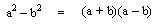
VIDEO DE FACTOR COMUN
VIDEO DE CUADRADOS PERFECTOS
VIDEO AGRUPACION DE TERMINOS
FACTOR COMUNJ POR AGRUPACION DE TERMINOS
Se llama factor común por agrupación de términos, si los términos de un polinomio pueden reunirse en grupos de términos con un factor común diferente en cada grupo.
Cuando pueden reunirse en grupos de igual número de términos se le saca en cada uno de ellos el factor común. Si queda la misma expresión en cada uno de los grupos entre paréntesis, se la saca este grupo como factor común, quedando así una multiplicación de polinomios.
Tratar desde el principio que nos queden iguales los términos de los paréntesis nos hará mas sencillo el resolver estos problemas.
2ax + 2bx - ay + 5a - by + 5b
Agrupo los términos que tienen un factor común:
(2ax - ay + 5a ) + ( 2bx - by + 5b )
Saco el factor común de cada grupo:
a ( 2x - y + 5 ) + b (2x - y + 5 )
Como las expresiones encerradas entre paréntesis son iguales se tiene:
( 2x -y +5 )(a + b)
Que es nuestra respuesta.
Ejemplos:
17ax – 17mx + 3ay - 3my + 7az – 7mz = a(17x +3y +7z) - m(17x + 3y +7z)
= (17x +3y +7z)(a – m)
m(x + 2) – x – 2 + 3(x + 2) = (x + 2)(m + 3) -1(x + 2) = (x + 2)[(m + 3) – 1]
= (x + 2)(m + 3 – 1)
DIFERENCIA DE CUADRADOS
Se le llama diferencia de cuadrados al binomio conformado por dos términos a los que se les puede sacar raíz cuadrada exacta.
Al estudiar los productos notables teníamos que:
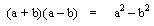
En donde el resultado es una diferencia de cuadrados, para este capítulo es el caso contrario:
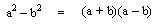
Donde siempre la diferencia de cuadrados es igual al producto de la suma por la diferencia de sus bases.
Pasos:
- Se extrae la raíz cuadrada de ambos términos.
- Se multiplica la suma por la diferencia de estas cantidades (el segundo termino del binomio negativo es la raíz del termino del binomio que es negativo).
Ejemplo explicativo:
VIDEO DE FACTOR COMUN
VIDEO DE CUADRADOS PERFECTOS
VIDEO AGRUPACION DE TERMINOS
